Allora... dopo tAAAnto lavoro adesso ho un p? di tempo per dedicarmi alle mie cose...
Cosa tiriamo fuori stavolta?
IL PIEGOMETRO!!!
eeeeh?
E che czz ? il PIEGOMETRO?
Serve a misurare di ste robe qua:

Agevolo spiegazioni per gli GNoranti... :gaen:
...ma prima un disclaimer sul post.
A cosa serve il post? A tre cose:
1) Fare del sano Soffoco Scientifico-TeNNologiko! :gaen:
2) A farvi rosicare perch? io cell'ho, e voi GNiente con la GN maiuscola!
3) W Biaggi! :1:
4) Boh? Non mi viene in mente...
Vabb?... iniziamo!
Per prima cosa dovete avere in mente gli angoli di Eulero.
zzo ? sta roba?
Niente di che... sono la descrizione matematica della posizione di un oggetto solido posto in uno spazio tridimensionale, RISPETTO ad un sistema di riferimento.
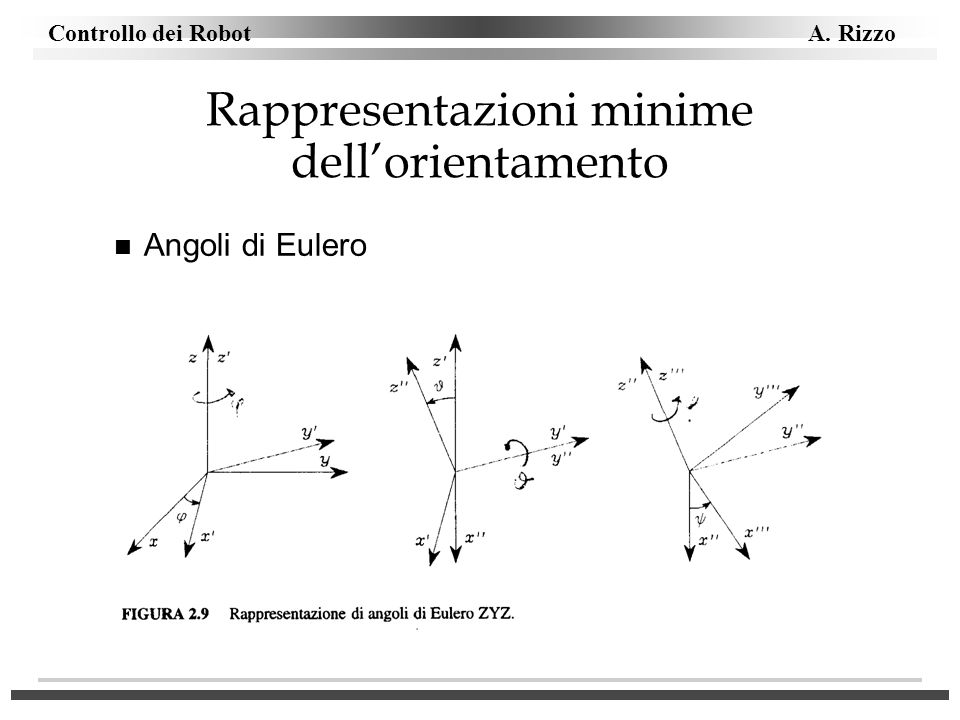
Per i rari normodotati:
Per le scimmie di Daidegas: Sono i tre angoli di quando vi piegate di lato, vi piegate in avanti (o indietro), oppure ruotate in tondo sui piedi intorno al vostro asse (tipo quando siete ubriachi).
Chiaro no?
Insomma, abbiamo degli angoli che possiamo definire inclinazioni rispetto ad un asse di riferimento che nel nostro caso sono l'orizzonte terrestre o, ancora meglio, l'asse perpendicolare alla direzione del vettore della gravit? terrestre.
In avionica detti angoli vengono definiti come:
1) ROLLIO (ROLL)
2) BECCHEGGIO (PITCH)
3) IMBARDATA (YAW)

Noi mutueremo questi termini aereonautici per i nostri usi...
1) ROLLIO = PIEGA SX-DX
2) BECCHEGGIO = IMPENNATA O ENDO
3) IMBARDATA = PERDITA DI CONTROLLO DELLA MOTO DURANTE UN HIGH SIDE = SPAVENTO
Nel nostro caso ci interessa conoscere unicamente l'angolo di ROLLIO, ovvero il coricamento laterale della moto, ma per i motivi che vedremo pi? avanti, ? necessario il calcolo di tutti gli elementi...
//**** IL PROGETTO
Il progetto consiste di due board separate, la prima delle quali ? una piattaforma inerziale a 6 assi, gestita da un DSP.
La seconda ? un sistema CPU-Display per la visualizzazione della misura dell'angolo.
La piattaforma inerziale (da questo momento IMU = Inertial-Measurement Unit)
? costutuita da un accelerometro a TRE assi, un doppio giroscopio a DUE assi per un totale d 4 assi, di cui solo TRE utilizzati, e controllati da un microprocessore con DSP engine, il quale significa che ? dotato di un potente motore per calcoli matematici frazionali.

Il visualizzatore ? costituito da un display grafico TFT da 3.2 pollici, pi? un processore di gestione di media capacit? (8 bit, 16 MHz)

//***** IL SOFTWARE
Innanzitutto qualcuno si chieder? come ? possibile ricavare un angolo da un acceleromentro attraverso un accelerometro, o ancora pi? strano, da un giroscopio. Lo spiegone ? questo (sintetico a prova di scimmia):
Gli accelerometri elettronici primncipalmente vengono costruiti con tecnologia MEMS, ovvero Micro Electro-Mechanical Systems.
Nello specifico, per l'elemento di misura, si tratta di un oggetto "disturbante" sospeso, che si muove tra matrici di armature costituenti dei condensatori. Spostandosi nello spazio altera la capacit? di questo o quel condensatore, dal quale si ricava il fattore di accelerazione, e non solo...
Immaginatevelo come una sferetta metallica sopesa in un cubo (le armature dei condensatori sono i sei lati).
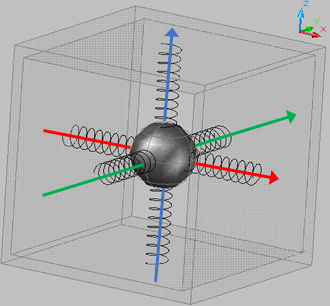
Ed ora qua viene la gabola...
Nell'immagine sopra vediamo la sfera perfettamente centrata nel cubo, ma... questo ? vero solo per forze di gravit? o accelerazioni (ricordiamoci che Einstein ha formulato che la Gravit? = accelerazione e viceversa, non per niente si chiama Accelerazione di Gravit?.... ) pari a ZERO.
) pari a ZERO.
In condizioni reali, ovvero con i piedi per terra, avremo una condizione pi? verosimile a questa:
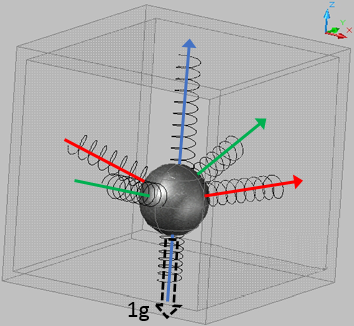
La sfera tende a scendere verso il basso a causa del suo peso (Gravit?), uscendo dalla sua condizione di perfetto e centrato equilibrio (in realt? trovando un nuovo equilibrio).
Adesso ruotiamo in avanti il cubo, e la nuova situazione sar? la seguente:
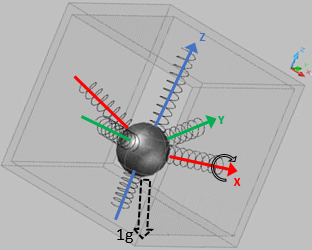
Ovvero la sferetta esce dalla sua condizione di equilibrio gravitazionale terrestre trovando un nuovo equilibrio di forze (come quando la vostra panza penzola in avanti, quando vi piegate per vomitare...).
I pi? furbi avranno gi? capito come sfruttare questo fenomeno per rivelare DUE dei tre angoli Euleriani...
...perch? solo due? Perch? se ruotiamo il cubo sul suo asse passante per l'asse di gravit?, la sferetta ruorter? anch'essa su suo asse ma senza pendere da nessuna parte (a parte alla gi? descritta flessione verso il centro della Terra). Ergo niernte angolo di IMBARDATA, ma solo ROLLIO E BECCHEGGIO.
Adesso servirebbe un p? di matematica per descrivere come si evincono tali angooli. In realt? trigonometria.
Sar? breve perch? ? una parte tediosa, ma giusto per capire du cazzate come funziona... (gli GNoranti saltino oltre... :gaen
Evitiamo robe cos?...

...e facciamola un p? pi? semplice...
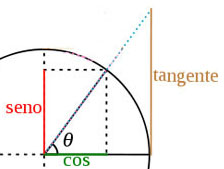
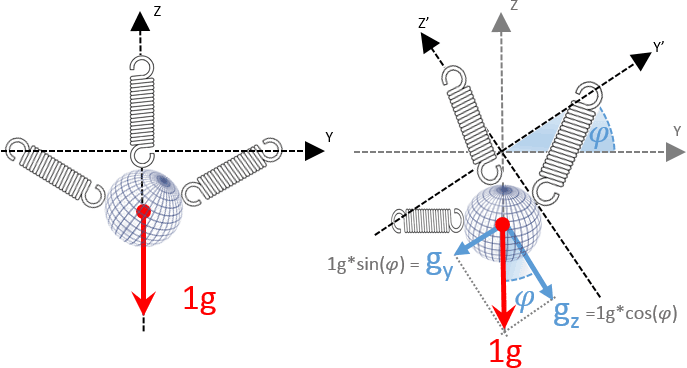
La forza che ora agisce sull’asse X (theta = θ) dell’accelerometro ? rappresentata dal segmento proiettato sul piano che chiamiamo AX che, in base al primo teorema dei triangoli rettangoli (un cateto ? uguale al prodotto dell’ipotenusa per il seno dell’angolo opposto o per il coseno dell’angolo adiacente) vale precisamente:
Ax = 1g * sen(θ)
Dato che stiamo ragionando sull’accelerazione statica, e 1g ? un termine unitario, per nostra comodit? lo omettiamo nelle descrizioni successive ma dovete tener conto che il valore di 1g ? comunque presente, altrimenti da un punto di vista dimensionale ? facile commettere degli errori (l’accelerazione ? misurata in g, ma il seno di un angolo ? un numero neutro, senza dimensioni):
Ax = sen(θ)
La formula inversa ci permette di ricavare l’angolo θ che l’asse X forma con l’orizzonte:
θ = arcsen(Ax)
Arcsen ? la funzione inversa del seno (arcoseno), e viene spesso anche indicata con sen-1. Ricordo che θ ? misurato in radianti, per avere il valore in gradi basta moltiplicarlo (IMPORTANTE!) per 180/Π
Utilizzando accelerometri ad un singolo asse, la sensibilit? (intesa in questo caso specifico come la variazione del valore in uscita dall’accelerometro in funzione della variazione dell’inclinazione) diminuisce sempre di pi? man mano che l’angolo aumenta: pi? ci avvicianiamo a ?90? e pi? una grande variazione di angolo si traduce in una piccola variazione di accelerazione. Perch?? Questo ? evidente dalla formula Ax = 1g * sen(θ) : l’accelerazione ? direttamente proporzionale al seno dell’angolo di inclinazione per cui di conseguenza la funzione ha un andamento sinusoidale:
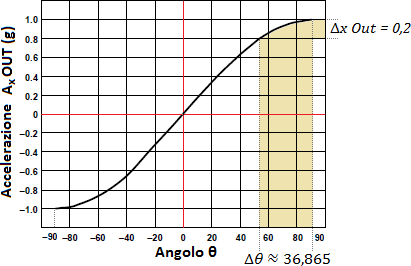
Per apprezzare quindi bene il valore dell’angolo in questi estremi ? necessario un accelerometro davvero molto sensibile altrimenti quando siamo prossimi ad un valore di angolo retto, il valore calcolato con la formula θ = arcsen(Ax) non fornisce un risultato preciso.
Un’altra forte limitazione dovuta all’utilizzo di un accelerometro a singolo asse ? data dal fatto che non ? possibile misurare valori di accelerazione a 360? dal momento che il valore misurato per un’inclinazione pari a N? ? lo stesso valore per un inclinazione pari a 180-N per cui non ? possibile distinguere l’inclinazione in un verso o nell’altro. Per alcune applicazioni pu? anche andar bene, per altre invece no.
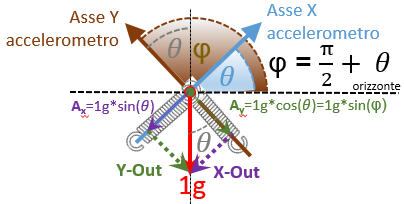
Per ovviare a questi “problemi” si ricorre ad un accelerometro a 2 assi ma anche ad un secondo accelerometro a singolo asse ma montato in maniera tale che l’asse di misura sia ortogonale all’asse di misura del primo accelerometro. Nel caso di un accelerometro a due assi, in caso di inclinazione avremo una situazione del genere:
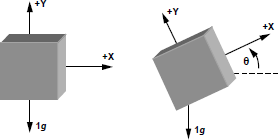
Vediamola da punto di vista euleriano:
In sintesi uso di un accelerometro a 2 assi (o anche integrando i due assi di un accelerometro triassiale) porta 2 vantaggi:
1) Abbiamo detto che con un solo asse la sensibilit? diminuisce man mano ci avviciniamo ad una inclinazione pari a ?90?. Questo continua ad essere vero anche con 2 assi, ma essendo questi assi ortogonali tra loro, quando la sensibilit? di un asse diminuisce, la sensibilit? dell’altro asse aumenta.
2) L’altro vantaggio di avere 2 assi ? quello che ora possiamo distinguere l’inclinazione in tutto l’arco dei 360? (con un solo asse era possibile stabilire, basandosi sul segno di Ax, solo se si ? nei quadranti in alto (I e II) o in basso (III e IV) :

Ecchill? l'integrazione dei due assi...
Adesso ? chiaro perch? servono due assi anche per avere una misura precisa di un solo asse.
E il giroscopio???
Il giroscopio per definizione ? un opggetto sensibile ai moti rotatori e misura la velocit? angolare. Anche in questo caso, integrando la velocit? angolare si pu? risalire all’angolo descritto. Usando una combinazione di accelerometri e giroscopi ? cos? possibile rilevare un movimento rototraslazionale vario.
E a che ci serve? Integrando la misura del giroscopio possiamo avere misure ancora pi? precise degli angoli euleriani.
Pi? in generale, accelerometri e giroscopi hanno capacit? e limiti che si compensano. Per esempio, il giroscopio subisce un fenomeno chiamato Drift (deriva) ma con un acceleromentro possiamo compensare questa deriva.
Dentro il micro DSP si processano tutti questi calcoli, oltre a vari filtri FIR sugli ingressi analogici per ridurre le figure di rumore, filtri di Kalman e un sacco di altre robe su cui ? megli soprassedere perch? in molti si saranno gio? rotti le balle e vogliono vedere il risultato...
Foto 1
Piattaforma inerziale:

Foto 2 - 3
Display:


Ho gi? smontato mezza moto per il montaggio, che entro Sabato deve essere teminato ASSOLUTAMENTE per il test probante, dove verr? testato sulle ultrastrade con pieghe da manicomio!
CONTINUA Eh!
Cosa tiriamo fuori stavolta?
IL PIEGOMETRO!!!
eeeeh?
E che czz ? il PIEGOMETRO?

Serve a misurare di ste robe qua:


Agevolo spiegazioni per gli GNoranti... :gaen:
...ma prima un disclaimer sul post.

A cosa serve il post? A tre cose:
1) Fare del sano Soffoco Scientifico-TeNNologiko! :gaen:
2) A farvi rosicare perch? io cell'ho, e voi GNiente con la GN maiuscola!
3) W Biaggi! :1:
4) Boh? Non mi viene in mente...
Vabb?... iniziamo!

Per prima cosa dovete avere in mente gli angoli di Eulero.
zzo ? sta roba?
Niente di che... sono la descrizione matematica della posizione di un oggetto solido posto in uno spazio tridimensionale, RISPETTO ad un sistema di riferimento.

Per i rari normodotati:
1.3 Angoli di Eulero
Date due generiche terne di riferimento ortogonali, orientate nello spazio
in modo qualsiasi, `e sempre possibile allineare una terna con l’altra attraverso
rotazioni successive.
Esistono sei diverse sequenze di rotazioni con cui `e possibile ottenere l’allineamento
delle terne e specificando una di esse, si descrive l’orientamento di una
terna rispetto all’altra. In particolare, quando si considerano gli assi verticalilocali
e gli assi corpo, si usa descrivere l’orientamento della seconda rispetto alla
prima mediante la sequenza di angoli di Eulero: φ, θ e ψ. In questo modo `e possibile
descrivere l’assetto di un velivolo, indicando il suo orientamento rispetto
agli assi verticali-locali.
Gli angoli di Eulero rappresentano tre rotazioni successive da eseguire intorno
agli assi di una terna inizialmente allineata con gli assi verticali-locali per allinearla
agli assi corpo. La prima rotazione avviene intorno all’asse Zv di un angolo
pari a ψ, detto angolo di imbardata (yaw angle), ottenendo una terna intermedia
T′ , il cui asse X′ `e allineato con la proiezione dell’asse Xb sul piano orizzontale
individuato dagli assi Xv Yv . La successiva rotazione avviene intorno all’asse Y ′
di un angolo pari a θ , detto angolo di beccheggio (pitch angle), ottenendo una
terna T′′ , il cui asse X′′ risulta definitivamente allineato con l’asse Xb. L’ultima
rotazione avviene intorno all’asse X′′ di un angolo pari a φ , detto angolo di rollio
(roll angle), che allinea completamente le due terne.
Gli angoli di Eulero, rappresentando le rotazioni da compiere per allineare gli
assi della terna verticale-locale con gli assi corpo, sono utilizzati per descrivere
l’assetto del velivolo.
Date due generiche terne di riferimento ortogonali, orientate nello spazio
in modo qualsiasi, `e sempre possibile allineare una terna con l’altra attraverso
rotazioni successive.
Esistono sei diverse sequenze di rotazioni con cui `e possibile ottenere l’allineamento
delle terne e specificando una di esse, si descrive l’orientamento di una
terna rispetto all’altra. In particolare, quando si considerano gli assi verticalilocali
e gli assi corpo, si usa descrivere l’orientamento della seconda rispetto alla
prima mediante la sequenza di angoli di Eulero: φ, θ e ψ. In questo modo `e possibile
descrivere l’assetto di un velivolo, indicando il suo orientamento rispetto
agli assi verticali-locali.
Gli angoli di Eulero rappresentano tre rotazioni successive da eseguire intorno
agli assi di una terna inizialmente allineata con gli assi verticali-locali per allinearla
agli assi corpo. La prima rotazione avviene intorno all’asse Zv di un angolo
pari a ψ, detto angolo di imbardata (yaw angle), ottenendo una terna intermedia
T′ , il cui asse X′ `e allineato con la proiezione dell’asse Xb sul piano orizzontale
individuato dagli assi Xv Yv . La successiva rotazione avviene intorno all’asse Y ′
di un angolo pari a θ , detto angolo di beccheggio (pitch angle), ottenendo una
terna T′′ , il cui asse X′′ risulta definitivamente allineato con l’asse Xb. L’ultima
rotazione avviene intorno all’asse X′′ di un angolo pari a φ , detto angolo di rollio
(roll angle), che allinea completamente le due terne.
Gli angoli di Eulero, rappresentando le rotazioni da compiere per allineare gli
assi della terna verticale-locale con gli assi corpo, sono utilizzati per descrivere
l’assetto del velivolo.
Chiaro no?

Insomma, abbiamo degli angoli che possiamo definire inclinazioni rispetto ad un asse di riferimento che nel nostro caso sono l'orizzonte terrestre o, ancora meglio, l'asse perpendicolare alla direzione del vettore della gravit? terrestre.
In avionica detti angoli vengono definiti come:
1) ROLLIO (ROLL)
2) BECCHEGGIO (PITCH)
3) IMBARDATA (YAW)

Noi mutueremo questi termini aereonautici per i nostri usi...
1) ROLLIO = PIEGA SX-DX
2) BECCHEGGIO = IMPENNATA O ENDO
3) IMBARDATA = PERDITA DI CONTROLLO DELLA MOTO DURANTE UN HIGH SIDE = SPAVENTO
Nel nostro caso ci interessa conoscere unicamente l'angolo di ROLLIO, ovvero il coricamento laterale della moto, ma per i motivi che vedremo pi? avanti, ? necessario il calcolo di tutti gli elementi...
//**** IL PROGETTO
Il progetto consiste di due board separate, la prima delle quali ? una piattaforma inerziale a 6 assi, gestita da un DSP.
La seconda ? un sistema CPU-Display per la visualizzazione della misura dell'angolo.
La piattaforma inerziale (da questo momento IMU = Inertial-Measurement Unit)
? costutuita da un accelerometro a TRE assi, un doppio giroscopio a DUE assi per un totale d 4 assi, di cui solo TRE utilizzati, e controllati da un microprocessore con DSP engine, il quale significa che ? dotato di un potente motore per calcoli matematici frazionali.

Il visualizzatore ? costituito da un display grafico TFT da 3.2 pollici, pi? un processore di gestione di media capacit? (8 bit, 16 MHz)

//***** IL SOFTWARE
Innanzitutto qualcuno si chieder? come ? possibile ricavare un angolo da un acceleromentro attraverso un accelerometro, o ancora pi? strano, da un giroscopio. Lo spiegone ? questo (sintetico a prova di scimmia):
Gli accelerometri elettronici primncipalmente vengono costruiti con tecnologia MEMS, ovvero Micro Electro-Mechanical Systems.
Nello specifico, per l'elemento di misura, si tratta di un oggetto "disturbante" sospeso, che si muove tra matrici di armature costituenti dei condensatori. Spostandosi nello spazio altera la capacit? di questo o quel condensatore, dal quale si ricava il fattore di accelerazione, e non solo...
Immaginatevelo come una sferetta metallica sopesa in un cubo (le armature dei condensatori sono i sei lati).

Ed ora qua viene la gabola...
Nell'immagine sopra vediamo la sfera perfettamente centrata nel cubo, ma... questo ? vero solo per forze di gravit? o accelerazioni (ricordiamoci che Einstein ha formulato che la Gravit? = accelerazione e viceversa, non per niente si chiama Accelerazione di Gravit?....
 ) pari a ZERO.
) pari a ZERO.In condizioni reali, ovvero con i piedi per terra, avremo una condizione pi? verosimile a questa:

La sfera tende a scendere verso il basso a causa del suo peso (Gravit?), uscendo dalla sua condizione di perfetto e centrato equilibrio (in realt? trovando un nuovo equilibrio).

Adesso ruotiamo in avanti il cubo, e la nuova situazione sar? la seguente:

Ovvero la sferetta esce dalla sua condizione di equilibrio gravitazionale terrestre trovando un nuovo equilibrio di forze (come quando la vostra panza penzola in avanti, quando vi piegate per vomitare...).
I pi? furbi avranno gi? capito come sfruttare questo fenomeno per rivelare DUE dei tre angoli Euleriani...
...perch? solo due? Perch? se ruotiamo il cubo sul suo asse passante per l'asse di gravit?, la sferetta ruorter? anch'essa su suo asse ma senza pendere da nessuna parte (a parte alla gi? descritta flessione verso il centro della Terra). Ergo niernte angolo di IMBARDATA, ma solo ROLLIO E BECCHEGGIO.
Adesso servirebbe un p? di matematica per descrivere come si evincono tali angooli. In realt? trigonometria.
Sar? breve perch? ? una parte tediosa, ma giusto per capire du cazzate come funziona... (gli GNoranti saltino oltre... :gaen
Evitiamo robe cos?...

...e facciamola un p? pi? semplice...

La forza che ora agisce sull’asse X (theta = θ) dell’accelerometro ? rappresentata dal segmento proiettato sul piano che chiamiamo AX che, in base al primo teorema dei triangoli rettangoli (un cateto ? uguale al prodotto dell’ipotenusa per il seno dell’angolo opposto o per il coseno dell’angolo adiacente) vale precisamente:
Ax = 1g * sen(θ)
Dato che stiamo ragionando sull’accelerazione statica, e 1g ? un termine unitario, per nostra comodit? lo omettiamo nelle descrizioni successive ma dovete tener conto che il valore di 1g ? comunque presente, altrimenti da un punto di vista dimensionale ? facile commettere degli errori (l’accelerazione ? misurata in g, ma il seno di un angolo ? un numero neutro, senza dimensioni):
Ax = sen(θ)
La formula inversa ci permette di ricavare l’angolo θ che l’asse X forma con l’orizzonte:
θ = arcsen(Ax)
Arcsen ? la funzione inversa del seno (arcoseno), e viene spesso anche indicata con sen-1. Ricordo che θ ? misurato in radianti, per avere il valore in gradi basta moltiplicarlo (IMPORTANTE!) per 180/Π
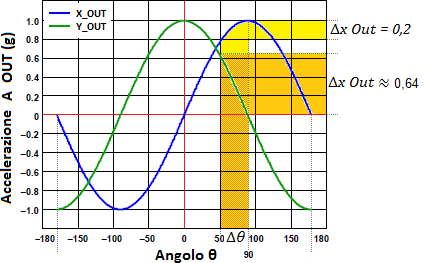
Utilizzando accelerometri ad un singolo asse, la sensibilit? (intesa in questo caso specifico come la variazione del valore in uscita dall’accelerometro in funzione della variazione dell’inclinazione) diminuisce sempre di pi? man mano che l’angolo aumenta: pi? ci avvicianiamo a ?90? e pi? una grande variazione di angolo si traduce in una piccola variazione di accelerazione. Perch?? Questo ? evidente dalla formula Ax = 1g * sen(θ) : l’accelerazione ? direttamente proporzionale al seno dell’angolo di inclinazione per cui di conseguenza la funzione ha un andamento sinusoidale:

Per apprezzare quindi bene il valore dell’angolo in questi estremi ? necessario un accelerometro davvero molto sensibile altrimenti quando siamo prossimi ad un valore di angolo retto, il valore calcolato con la formula θ = arcsen(Ax) non fornisce un risultato preciso.
Un’altra forte limitazione dovuta all’utilizzo di un accelerometro a singolo asse ? data dal fatto che non ? possibile misurare valori di accelerazione a 360? dal momento che il valore misurato per un’inclinazione pari a N? ? lo stesso valore per un inclinazione pari a 180-N per cui non ? possibile distinguere l’inclinazione in un verso o nell’altro. Per alcune applicazioni pu? anche andar bene, per altre invece no.
Per ovviare a questi “problemi” si ricorre ad un accelerometro a 2 assi ma anche ad un secondo accelerometro a singolo asse ma montato in maniera tale che l’asse di misura sia ortogonale all’asse di misura del primo accelerometro. Nel caso di un accelerometro a due assi, in caso di inclinazione avremo una situazione del genere:

Vediamola da punto di vista euleriano:

In sintesi uso di un accelerometro a 2 assi (o anche integrando i due assi di un accelerometro triassiale) porta 2 vantaggi:
1) Abbiamo detto che con un solo asse la sensibilit? diminuisce man mano ci avviciniamo ad una inclinazione pari a ?90?. Questo continua ad essere vero anche con 2 assi, ma essendo questi assi ortogonali tra loro, quando la sensibilit? di un asse diminuisce, la sensibilit? dell’altro asse aumenta.
2) L’altro vantaggio di avere 2 assi ? quello che ora possiamo distinguere l’inclinazione in tutto l’arco dei 360? (con un solo asse era possibile stabilire, basandosi sul segno di Ax, solo se si ? nei quadranti in alto (I e II) o in basso (III e IV) :

Ecchill? l'integrazione dei due assi...

Adesso ? chiaro perch? servono due assi anche per avere una misura precisa di un solo asse.
E il giroscopio???
Il giroscopio per definizione ? un opggetto sensibile ai moti rotatori e misura la velocit? angolare. Anche in questo caso, integrando la velocit? angolare si pu? risalire all’angolo descritto. Usando una combinazione di accelerometri e giroscopi ? cos? possibile rilevare un movimento rototraslazionale vario.
E a che ci serve? Integrando la misura del giroscopio possiamo avere misure ancora pi? precise degli angoli euleriani.
Pi? in generale, accelerometri e giroscopi hanno capacit? e limiti che si compensano. Per esempio, il giroscopio subisce un fenomeno chiamato Drift (deriva) ma con un acceleromentro possiamo compensare questa deriva.
Dentro il micro DSP si processano tutti questi calcoli, oltre a vari filtri FIR sugli ingressi analogici per ridurre le figure di rumore, filtri di Kalman e un sacco di altre robe su cui ? megli soprassedere perch? in molti si saranno gio? rotti le balle e vogliono vedere il risultato...

Foto 1
Piattaforma inerziale:

Foto 2 - 3
Display:


Ho gi? smontato mezza moto per il montaggio, che entro Sabato deve essere teminato ASSOLUTAMENTE per il test probante, dove verr? testato sulle ultrastrade con pieghe da manicomio!
CONTINUA Eh!





Comment